О СУЩНОСТИ ЭНТРОПИИ В ДОМАШНИХ УСЛОВИЯХ
И ТЕОРИИ ОБОБЩЕННОГО ВРУНА
ВМЕСТО ПРЕДИСЛОВИЯ
Прежде всего хотелось бы отметить, что вся эта по сути дела статья – не есть плод больного воображения. Все, представленное здесь, – правда. При создании статьи я опирался не только на собственные знания информатики за школьный курс, но и на статью Воронцова А.В. «Информация, энтропия и обобщенные вруны», напечатанную в журнале «Потенциал» за январь 2005 года. Большинство примеров задач также взяты оттуда. Ну, вроде бы все. Итак, lets go!
Глава 1. Школьные задачи
Я не буду говорить о том, что такое информация, в чем ее измеряют и что такое количество информации. Все это (по умолчанию) вы должны уже знать (у кого в школе информатики не было – возьмите любой учебник по информатике за первый год изучения этого предмета). Напомню только, что количество информации измеряется в битах, а бит – двоичный символ – 1 или 0, «да» или «нет», «черный» либо «белый» и так далее.
Все учащиеся на уроках информатики сталкивались с «простыми» задачами. Вот пример: «Гриша сказал, что следующий урок – математика. До этого Петя знал, что следующий урок либо математика, либо физика, либо ОБЖ, либо химия. Сколько бит информации получил Петя?»
Задача просто решается, если вспомнить формулу:
I=log2N,
где N – количество комбинаций, I – количество информации (разрядов). Тогда решение
задачи выглядит следующим образом:
«Количество возможных вариантов следующего урока равно 4.
I=log24=2
Ответ: 2 бита.»
Другой пример: «Есть шахматная доска 8х8.
Сколько надо двоичных разрядов, чтобы закодировать одну клетку?» Здесь вообще-то
надо использовать другую формулу –
I=logaN,
где а – основание системы счисления. В нашем случае говорят о двоичных разрядах
(битах), следовательно а=2. Тогда
I=log264=6,
Ответ: 6 бит.
В зависимости от задачи, все переменные (I,N,a)
могут меняться. Также можно усложнить и сами задачи:
«У Васи есть одна доминошка. Он признался,
что у него дубль. Сколько информации он сообщил?»
«Коля съел на перемене яблоко, конфету и кекс. Сколько элементарных вопросов надо
задать, чтобы узнать, в какой последовательности он их съел? Сколько информации
от нас скрыто? А если объектов было 6?»
Для решения второй задачи необходимо понимать,
что элементарный вопрос – это тот вопрос, на который ответ мы получаем «да» или
«нет», т.е. 1 бит информации.
Но все это – школьные задачи. А теперь – самое
интересное…
Глава 2. Энтропия
Сразу предупреждаю, что если первая глава
была вполне понятная, то во вторую «въехать» будет куда сложнее, если нет основательно
подготовленной базы знаний по математике. И все же попробуем… А если непонятно
что-то - просто просмотрите эту главу, и переходите к третьей. Она попроще.
Итак, что такое энтропия? Начну «издалека».
Как нетрудно догадаться, основная функция информации – уменьшать «незнание» (знаю,
что корявое слово). Другими словами, информация – это мера уменьшения неопределенности.
Так вот, а сама степень неопределенности – это и есть энтропия. Все? Как бы не
так! Количество информации определили через формулу, значит, должны как-то определить
энтропию. Пристегнулись? Полетели!
Разберем задачу. «Перед нами 5 черных ящиков.
В каждом из них находится либо черный, либо белый шар. Мера неизвестности (неизвестной
информации) равна 5 бит. Нам говорят, что 3 шара белые. Сколько информации нам
сообщили? Сколько нам осталось узнать?»
Решение. Сначала было 32 варианта, т.к. мера
неизвестности равнялась 5=log 232. Когда нам сказали, что
3 шара белые, число возможных вариантов стало равно количеству возможных распределений
3 белых и 2 черных шаров в 5 ящиках. Их 10 штук (1 – белый, 0 – черный):
11100, 11010, 11001,10110, 10101, 10011, 01110, 01101, 01011,
00111.
Это число распределений равно
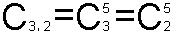
и называется также числом сочетаний 3 элементов из 5, или 2 элементов из 5,
или биноминальным коэффициентом (2,3). (Вы не знаете, что такое сочетания? К
сожалению, это довольно большая тема, и сейчас ее отразить невозможно. Поищите
в учебниках по математике в ВУЗах в разделе комбинаторики или посмотрите здесь, в статье "Кодовый замок как способ защитить подъезд", в главе "КОМБИНАТОРИКА". Только, боюсь, этого не хватит). Это число С3,2
=10 получается так: первый нолик можно поместить в любое из 5 мест, второй –
в любое из 4. Всего получается 20 вариантов, но 10 из них для мест первого нолика,
а 10 – для второго. А нам какая разница? А тогда вариантов 10. Было неизвестно
5 бит, потом стало неизвестно log 2(С3,2)=
log 210=3.32 бит, Значит нам сообщили 5 - log 210=1.68
бит информации.
А теперь обобщим задачу.
«Перед нами n ящиков. В каждом из них либо
белый, либо черный шар. Нам говорят, что 60% из них – белые. Сколько информации
нам осталось узнать, т.е. чему равна мера незнания?»
По аналогии с предыдущим случаем для n=100
получаем log 2(С60,40),
для n=1000 - log 2(С600,400),
в общем случае - log 2(С0.6n,0.4n).
Теперь подробнее рассмотрим число Сm,n
. По сути дела это способ разместить n единичек и m ноликов по n+m местам. Для
вычисления общей формулы Сm,n
лучше использовать формулу Сm,n
= Сm-1,n + Сm,n-1
. Но как это считать? Есть такая штука – треугольник Паскаля. Каждое число в
нем – это сумма двух стоящих над ним. Чтобы узнать, чему равно Сm,n
, надо взглянуть на n+m строчку. На первом месте всегда 1 – это Сm+n,0
, число способов размещения n+m единичек по n+m местам.
Далее Сm+n-1,1 , число способов
разместить n+m-1 единичек и 1 нолик в n+m местах (например, С4,1
= 5. Не верите – проверьте). И так далее до Сm,n.

А теперь самое «веселое»! Когда p*n, 0<p<1,
из неизвестных нам n бит есть единички, мера нашего незнания, изначально равная
n, уменьшается до log 2(Сp*n,(1-p)*n).
Мера нашего незнания умножается на число, меньшее 1, равное log 2(Сp*n,(1-p)*n)/n.
Обозначим это выражение Нn(p). Это число можно назвать
незнанием, приходящимся на каждый бит. Или так: сколько информации нам осталось
узнать про каждый бит после того, как нам сказали, что p*100% бит равны 1. Тогда
энтропией случайной величины с вероятностями
{p, p-1} называется функция Нn(p) = -(p*log 2p
+ (1-p)* log 2(1-p)).
Причем чем больше n, тем более схожи функции
Нn(p) и функция энтропии Н(p). Выбирая большие n, мы
можем их сделать сколь угодно мало отличающимися в каждой точке.
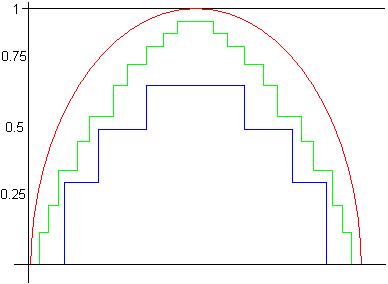
Красным цветом обозначен график функции
Н(р)
Графики функции Нn(p)
= log 2(Сp*n,(1-p)*n)/n:
при n=7 - синий,
при n=28 - зеленый.
Последние слова об энтропии. Случайная величина
с вероятностями p1, p2, p3, где p1+p2+p3=1 имеет энтропию Н({p1,p2,p3})= -(p1*log
2p1 + p2*log 2p2 + p3*log 2p3)=
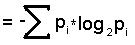
,где i = 3, а сама формула – это общая формула
энтропии случайной величины.
Глава 3. Обобщенные вруны
Если вы выжили после предыдущей главы, то
эта покажется пустяком – математики здесь не так много. Начали!
Вернемся к элементарным вопросам. Задача.
«Из первых 16 чисел Вася одно загадал. Сколько вопросов понадобиться, чтобы угадать
это число? Вопросы элементарные». Решать надо так: «Первый вопрос. Верно ли, что
число меньше 9? Пусть да. Тогда второй вопрос: верно ли, что число меньше 5? И
так далее. Не трудно заметить, что нужно 4 вопроса:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 2 3 4 5 6 7 8
1 2 3 4
1 2
2
1
Это решение задачи для всех ответов «Да».
И тут выползает «НО»…
НО если человек, который отвечает, говорит неправду (врет). Если
он врет всегда (т.е. является абсолютным вруном), то ничего страшного нет –
надо лишь все его ответы воспринимать наоборот. Но такого вруна еще поискать
надо! А обыкновенные вруны врут в n% случаях. Это и есть обобщенные вруны. Можно
ли у такого вруна узнать правду? Да. А как?
Для начала нам понадобится такая величина,
как пропускная способность обобщенного вруна. Это то, сколько бит выданной этим
вруном информации в среднем приходится на один вопрос.
Итак, пусть у нас есть обобщенный 40% врун
(т.е. он врет в 40% случаях). Зададим ему n элементарных вопросов. Мы знаем,
что на 40% вопросов он соврал. Информация о том, на какие вопросы именно он
соврал представляет собой n*Н(0.4) бит. Предположим, что мы задали вопросы так,
что в полученных n ответах содержится нужная нам перевранная информация размером
m бит и еще информация о том, в каких именно вопросах он соврал. То есть m+n*Н(0.4)=n
или m=n-n*Н(0.4)=n*(1-Н(0.4)) и пропускная способность вруна равна V=m/n=1-H(p)
А какой от этого прок?- спросит кто-нибудь.
Хочется посоветовать этому человеку не задавать таких вопросов больше… Но все
же прок есть – полученная формула означает, что, если умель задавать вопросы,
то за n вопросов у р% вруна можно веведать n*V=n*(1-H(p)) бит.
Ну и на закуску. На рисунках представлена
геометрическая интерпретация пропускной способности – это отрезок АВ. В первом
случае врун симметричный, т.е. он врет на ответах и «Да» и «Нет» с одинаковой
вероятностью р. Второй случай – это несимметричный врун. Когда надо отвечать
«Да», он врет с вероятностью a, когда «Нет» - с вероятностью b.
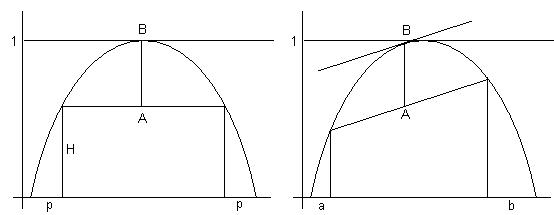
P.S. Если врун в обоих случаях врет с вероятностью
0.5, то мы никогда у него ничего не узнаем… Увы!